 En el esquema, A es la enzima, B1 y B2 son los sustratos.
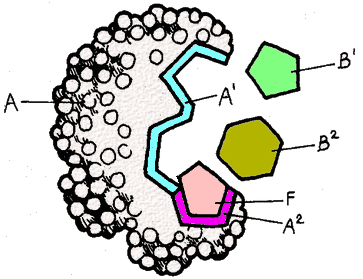
En el esquema, A es la enzima, B1 y B2 son los sustratos. ¿Qué tipo de inhibición ejerce el compuesto representado por el pentágono rosado (F)?
a) ¿Cuáles son los aspectos característicos de las reacciones enzimáticas? ¿Qué propiedades presentan las enzimas que las diferencian de otros catalizadores?
b) ¿Es cierto que todas las enzimas conocidas son de naturaleza polipeptídica?
c) ¿Qué tipo de interacciones se ejercen entre la enzima y el sustrato para formar el complejo ES?
d) ¿Bajo qué condiciones podemos asegurar que medimos velocidades iniciales? ¿Puede medirse velocidad inicial fuera de estas condiciones?
a) Capacidad de acelerar mucho la reacción, desde 106 hasta 1018 veces. Elevada especificidad por un sustrato.
b) No. Algunas enzimas son moléculas de RNA. Se las llama ribozimas.
c) Interacciones débiles no covalentes (iónicas o electrostáticas, enlaces de hidrógeno, enlaces de Van der Waals, efecto hidrófobo). En algunos caso, la enzima o su coenzima forman un enlace covalente con el intermediario de reacción, que luego se revierte regenerando la enzima intacta.
d) Cuando la concentración del producto es aún muy baja.
 En el esquema, A es la enzima, B1 y B2 son los sustratos.
En el esquema, A es la enzima, B1 y B2 son los sustratos.
¿Qué tipo de inhibición ejerce el compuesto representado por el pentágono rosado (F)?
La unión del inhibidor F impide la unión del sustrato B2, y viceversa. Por lo tanto, compiten (respuesta a)
Se desea medir la actividad de una enzima de tipo esterasa que actúa sobre butirato de etilo. Una forma de seguir el curso de la reacción es midiendo el consumo de NaOH necesario para mantener el pH constante en 8.5.
¿Cómo definirías una unidad (arbitraria) de actividad para esta enzima?
La reacción será butirato de etilo ![]() ácido butírico + etanol
ácido butírico + etanol
El butírico está siendo neutralizado por la adición de NaOH descrita.
En consecuencia, la cantidad de NaOH añadida es equivalente a la cantidad de producto y podemos definir la velocidad como moles de NaOH consumidos por unidad de volumen y de tiempo.
Se ha medido la actividad de una preparación de invertasa en 10 ml totales de una mezcla de reacción con sacarosa 0.2 M y tampón acetato 20 mM, pH=4.77 (Km = 61 mM). Al cabo de 20 minutos se han hidrolizado 18 µmol de sustrato. Calcula la concentración de actividad enzimática en la muestra.
[AE] = 18 µmol / ( 10 ml × 20 min ) = 90 µM/min = 90 U/L
I |
II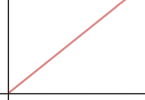 |
III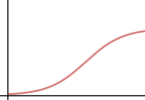 |
|
IV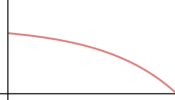 |
V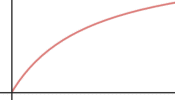 |
||
Para una reacción catalizada por una enzima micaeliana:
a) Dibuja cómo varía la velocidad de la reacción en función del tiempo que pasó desde que se inició.
b) Haz lo mismo para la velocidad inicial en función de la concentración de sustrato.
c) Traza una gráfica de velocidad inicial frente a concentración de enzima.
a) respuesta IV: Para tiempos cortos la velocidad de reacción es constante; a tiempos mayores, a medida que el sustrato se va consumiendo, la velocidad decrece.
b) respuesta V: Para concentraciones bajas de sustrato la velocidad aumenta linealmente con la concentración; para concentraciones más altas la velocidad aumenta menos, hasta hacerse casi constante (saturación de los sitios activos de la enzima)
c) respuesta II: La velocidad inicial aumenta proporcionalmente a la concentración de enzima. La gráfica es una recta.
a) ¿Qué es la constante de Michaelis?
b) Define kcat
c) ¿Qué es el número de recambio?
d) (Avanzada) ¿Cómo varía la velocidad inicial para [S]<<Km y para [S]>>Km?
a) Se puede definir de varias formas: (a) una combinación de constantes de velocidad de formación y desaparición del complejo E·S; (b) el valor de concentración de sustrato que proporciona la mitad de la velocidad máxima de catálisis; (c) el valor de concentración de sustrato para el cual están ocupados la mitad de los sitios activos de la enzima.
b) El nº de moléculas de sustrato convertidas en producto por un solo centro activo, por unidad de tiempo. En el modelo de Michaelis y Menten coincide con la constante de velocidad de la conversión del complejo E·S en producto.
c) Lo mismo que kcat (pregunta anterior).
d) Para [S]<<Km la velocidad inicial de reacción es proporcional a la concentración de sustrato (lo que se conoce como cinética de orden uno). Para [S]>>Km la velocidad inicial de reacción es independiente de la concentración de sustrato (cinética de orden cero)
La Km de cierta enzima por su sustrato es 1.0×10−5 M. La reacción sigue la cinética de Michaelis y Menten. Para una determinada concentración de enzima y una concentración de sustrato de 0.1 M, la velocidad inicial de reacción fue 37 µM/min. A una concentración de sustrato 0.01 M la velocidad inicial de reacción es también 37 µM/min.
a) ¿Por qué esta reducción de 10 veces en la concentración de sustrato no tiene efecto sobre la velocidad inicial de reacción?
b) Demuéstralo usando cálculos numéricos.
a) En ambos casos la [S] es muy superior a la Km, por lo que la enzima está saturada con sustrato y la velocidad medida se aproxima mucho a la máxima
b) los valores son indistinguibles en la práctica:
caso 1) ѵ = ѵmáx × 0.1 M / (1.0×10−5 M + 0.1 M) = ѵmáx × 0.99990001
caso 2) ѵ = ѵmáx × 0.01 M / (1.0×10−5 M + 0.01 M) = ѵmáx × 0.999001
| Km | ѵmáx | |
|---|---|---|
| isoenzima | (mM) | (µM/min) |
| A | 2.0 | 400 |
| B | 0.5 | 80 |
| C | 0.1 | 35 |
La tabla muestra los resultados obtenidos al determinar Km y ѵmáx para 3 isoenzimas. En todos los casos se utilizaron las mismas condiciones de reacción (pH, T, fuerza iónica), el volumen final de la reacción fue de 10 ml y se agregó enzima hasta una concentración final de 10 pM.
a) ¿Qué isoenzima muestra más afinidad por el sustrato?
b) ¿Cuál de las 3 isoenzimas tiene mayor número de recambio?
a) La isoenzima "C" (tiene menor Km, une más sustrato para una concentración dada)
b) El nº de recambio es kcat. Lo tiene mayor la que muestre mayor ѵmáx, es decir, la isoenzima "A"
La tabla indica el valor de la constante de Michaelis para dos enzimas cuyo sustrato son aminoácidos.
| enzima | Km |
|---|---|
| aminoacil-tRNA sintetasas (EC 6.1.1.x) | 2.2 µM |
| transaminasas (EC 2.6.1.x) | 30 mM |
A. Razona: ¿qué enzima trabajará a plena capacidad en las siguientes condiciones?
a) Cuando la concentración de aminoácidos en una célula está en torno a 0.02 mM
b) Si la concentración de aminoácidos en una célula se eleva a 20 mM
B. La función de las aminoacil-tRNA sintetasas es utilizar los aminoácidos para sintetizar proteínas, mientras que la de las transaminasas es degradar los aminoácidos. Razona cuál de estos procesos será activo en cada una de las dos condiciones anteriores y por qué tal situación es adecuada fisiológicamente para el organismo.
A)a) Para 20 µM las sintetasas están bastante por encima de su Km, por lo cual trabajan cerca de saturación, cerca de su velocidad máxima. Por el contrario, las transaminasas están muy por debajo de su Km y actuarán con una velocidad muy baja.
A)b) A esa concentración las sintetasas siguen trabajando a saturación, mientras que las transaminasas ya transforman los aminoácidos a velocidad apreciable.
B) Cuando hay poca cantidad de aminoácidos, se utilizan para sintetizar proteínas y no se degradan. Sólo se destinan a degradación cuando su concentración es muy elevada; los aminoácidos no se usan como fuente de energía habitualmente.
La tabla indica el valor de la constante de Michaelis para dos enzimas cuyo sustrato es la glucosa y que catalizan la misma reacción.
| enzima | Km | kcat |
|---|---|---|
| glucoquinasa (EC 2.7.1.2) | 10 mM | alta -- 62 s−1 |
| hexoquinasa (EC 2.7.1.1) | 100 µM | baja -- 60-100-318 ?? s−1 |
A. Razona: ¿qué enzima trabajará a plena capacidad en las siguientes condiciones?
a) En situación de hipoglucemia, la concentración de glucosa en todos los tejidos es baja (~120 µM).
b) Tras una comida rica en carbohidratos, la glucemia en la vena porta es elevada (12 mM) y de ahí la glucosa puede entrar a los hepatocitos antes de distribuirse por el organismo.
B. Una de las funciones de los hepatocitos es almacenar reservas en forma de glucógeno (un polímero de glucosa), mientras que el resto de tejidos utilizan la glucosa como combustible, para oxidarla y obtener energía. Razona de qué modo la presencia de glucoquinasa exclusivamente en los hepatocitos se adecúa a una funcionalidad fisiológica.
A)a) La glucoquinasa está muy por debajo de su Km, por lo que tiene poca actividad sobre la glucosa. La hexoquinasa, en cambio, tendrá alta actividad.
A)b) La hexoquinasa en estas condiciones sí puede actuar eficazmente sobre la glucosa.
B) En consecuencia, con glucemia elevada el hígado capta el exceso de glucosa de la vena porta y la fosforila (para almacenarla en forma de glucógeno), mientras que cuando la glucemia es baja el hígado no usa la glucosa y la deja disponible para los demás tejidos (que la usarán como fuente de energía).
La glucoquinasa cataliza la reacción glucosa + ATP ![]() glucosa-6-fosfato + ADP
glucosa-6-fosfato + ADP
El curso de la reacción se puede seguir colorimétricamente por el método de Somogyi-Nelson (titulación de glucosa remanente no fosforilada, previa precipitación de la glucosa-6P como sal de bario). Se midió la actividad de una preparación de glucoquinasa en una mezcla de reacción de 1 ml que contenía 0.4 ml de glucosa 0.01 M, 0.05 mg de enzima, suficiente Mg2+, ATP en exceso, todo en un tampón de pH=7.0.
a) Si a los 3 minutos quedaron 3.91 µmol de glucosa por ml de mezcla de reacción, calcula la velocidad inicial de la reacción expresada en µmol de glucosa transformada por minuto.
b) Calcula la ѵmáx sabiendo que Km = 0.8×10−2 M.
c) Calcula la cantidad total de glucosa fosforilada en los primeros 6 minutos, cuando la mezcla de reacción se prepara con 0.6 ml de glucosa 0.01 M y 0.05 mg de enzima.
a) Sustrato de partida: 4 µmol; final: 3.91 µmol; sustrato convertido en producto (en 3 min): 0.09 µmol. ѵ0 = 0.03 µmol/min
b) Asumiendo comportamiento michaeliano, se cumplirá la ecuación para el único punto que se ha determinado:
ѵmáx = ѵ × ([S] + Km) / [S] = 0.03 µmol/min × (4 mM + 8 mM) / 4 mM = 0.09 µmol/min
o bien en concentración, 0.09 mM/min
c) la nueva [S] = 6 mM; ѵ = ѵmáx × [S] / ([S] + Km) = 0.09 mM/min × 6 mM / (6 mM + 8 mM) = 38.6 µM/min
en 6 min y 1 ml: mGlc = 38.6 µM/min × 6 min × 1 ml = 0.2316 µmol
Para resolver los siguientes problemas será necesario hacer una regresión de los datos a la ecuación de Michaelis y Menten. Usad para ello un método de regresión no lineal a la curva hiperbólica, como el disponible en Biomodel.
| [sustrato] | ѵ0 |
|---|---|
| (µM) | (nM/min) |
| 500 | 62 |
| 100 | 54 |
| 50 | 41 |
| 30 | 33 |
| 20 | 28 |
| 10 | 15 |
| 5 | 9.5 |
| 1 | 2.2 |
| 0.5 | 1.1 |
En 10 mezclas de reacción con la misma concentración de enzima y distintas concentraciones de sustrato, se determinaron las velocidades iniciales, obteniéndose los datos que se muestran en la tabla.
Determina los valores de ѵmáx y Km para esta enzima con su sustrato.
ѵmáx = 67 µM ±1; Km = 30 nM/min ±2
| [sustrato] | ѵ0 |
|---|---|
| (µM) | (µM/min) |
| 500 | 24.5 |
| 50 | 19.7 |
| 5.0 | 7.15 |
| 0.5 | 0.96 |
Se estudió el efecto de la concentración de sustrato sobre la velocidad de una reacción enzimática. Se midieron las velocidades iniciales para distintas concentraciones de sustrato, con una concentración constante de enzima, en un volumen total de 10 mL. Se obtuvieron los resultados reflejados en la tabla.
a) Calcula cuáles son los valores de ѵmáx y Km de esta enzima para este sustrato.
b) ¿Cuáles serían las velocidades iniciales para [S]=1.0×10−6 M y 1.0×10−1 M?
c) Si la concentración de enzima en cada mezcla de reacción se incrementase 4 veces, ¿cuál sería el nuevo valor de Km? ¿y el de ѵmáx? ¿Cuál sería el nuevo valor de ѵ0 para [S]=5.0×10−6 M?
d) (avanzado) Calcula la cantidad total de producto formado durante los primeros 5 minutos cuando [S]=2.0×10−3 M. ¿Es posible hacer el mismo cálculo para [S]=2.0×10−6 M? ¿Por qué?
a) ѵmáx = (25.0 ± 0.2) µM/min ; Km = (12.8 ± 0.5) µM
b) usando la ecuación de MM: (b1) ѵ0 = 1.81 µM/min ; (b2) ѵ0 = 25.0 µM/min
c1) Km no cambia, es una propiedad intrínseca de la enzima para su sustrato;
c2) ѵmáx sería el cuádruple, 100 µM/min
c3) usando la ecuación de MM con ѵmáx = 100 µM/min , se obtiene ѵ = 28.1 µM/min
d) ѵ0 = 24.8 µM/min; asumiendo que se haya mantenido esa velocidad inicial durante los 5 min, se producen
24.8 µM/min × 10×10−3 L × 5 min = 1.24 µmol de producto
La cantidad de S disponible inicialmente era 2.0×10−3 M × 10×10−3 L = 2.0×10−5 mol = 20 µmol
por lo tanto, es factible que se haya gastado ese sustrato a esa velocidad.
Sin embargo, partiendo de 2.0×10−6 M de S habrá 20×10−3 µmol iniciales
y
es imposible transformar 1.24 µmol: el sustrato se agota antes de los 5 min.
| [sustrato] | ѵ0 |
|---|---|
| (µM) | (nM/min) |
| 6.25 | 15.01 |
| 70.0 | 58.25 |
| 100 | 59.12 |
| 500 | 74.90 |
Los datos reflejados en la tabla se midieron para una reacción S ![]() P catalizada enzimáticamente.
P catalizada enzimáticamente.
a) Determina los valores de ѵmáx y Km.
b) ¿Cuál sería ѵ0 si [S] = 2.0×10−5 M? ¿Y para [S] = 5.0×10−5 M?
c) ¿Cómo cambiaría la velocidad para [S] = 5.0×10−5 M si la concentración de enzima es el doble de la original?
d) ¿Cuál es la fracción de sitios activos desocupados cuando [S] es 1.0×10−2 M? ¿Y cuando [S] es 6.25×10−6 M?
e) (avanzada) Las velocidades de la tabla se calcularon midiendo la concentración de producto acumulado en un período de 10 min. ¿Es válida la suposición de que estos valores de ѵ representan las velocidades iniciales en todo el intervalo de [S] utilizado?
a) ѵmáx = 78 nM/min ±3; Km = 27 µM ±4
b) usando la ecuación de Michaelis y Menten: ѵ0 = 33.2 y 50.6 nM/min
c) doble: 101.2 nM/min
d) Para el primer caso, [S] = 104 µM y está en saturación, fracción=0, todo está ocupado
La fracción ocupada equivale a ѵ/ѵmáx es decir, en el segundo caso, 15.01/78 = 0.192, está desocupado el 81% de los sitios
e) Debemos asegurarnos de que hay exceso de sustrato, de que no se agota antes de los 10 min
Se pretende medir los parámetros cinéticos de la enzima invertasa de un extracto de levadura comercial. Esta enzima cataliza la siguiente reacción:
sacarosa + H2O ![]() glucosa + fructosa
glucosa + fructosa
Para ello, se diseñó el experimento esquematizado en la tabla I.
| Mezcla de reacción | 1 | 2 | 3 |
|---|---|---|---|
| tampón acético / acetato sódico 0.02 M, pH=4.77 | 2 ml |
2 ml |
2 ml |
| sacarosa 0.5 M | - |
- |
2 ml |
| sacarosa 0.05 M | 2 ml |
4 ml |
- |
| extracto enzimático | 0.4 ml |
0.4 ml |
0.4 ml |
| agua | 5.6 ml |
3.6 ml |
5.6 ml |
| Tiempo de reacción (min) |
Cantidad de glucosa (µmol) | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| 2 | 1.6 |
2.0 |
3.0 |
| 5 | 3.7 |
4.5 |
9.0 |
| 7 | 5.5 |
6.3 |
12.6 |
| 10 | 5.5 |
9.0 |
18.2 |
Las tres mezclas de reacción se incubaron a 20°C, tomándose muestras de 1 ml a 2, 5, 7 y 10 min de iniciada la incubación. Sobre las muestras se determinó la cantidad de glucosa formada (tabla II).
a) Calcula ѵmáx y Km para esta enzima con sacarosa como sustrato.
b) Calcula la actividad enzimática invertasa presente en los 0.4 ml de extracto enzimático.
Lo primero es calcular la concentración de sustrato y la velocidad de reacción en cada tubo.
t1: 10 mM, 80 µM/min
t2: 20 mM, 100 µM/min
t3: 100 mM, 150 µM/min
Nota: para las velocidades iniciales lo más razonable (aunque aproximado) es usar el primer dato, de 2 min. Otra solución más correcta sería trazar las curvas frente al tiempo y obtener la pendiente inicial (tangente a la curva)
a) Con ello se obtienen por regresión ѵmáx= 166 µM/min ±9 y Km =12 mM ±2
b) La actividad, entendida como velocidad de conversión de sustrato, depende de la concentración de éste. Debemos, pues, interpretar que para medir la actividad como indicador de la presencia de una enzima no debe haber condiciones limitantes de la reacción, es decir, debe haber exceso de sustrato, la enzima debe estar saturada. Por lo tanto, usamos el valor de ѵmáx y la [AE] = 166 µM/min en las condiciones del ensayo
La actividad enzimática en los 0,4 ml de muestra original será AE = 166 µM/min × 10 ml = 1.66 µmol/min
(y la concentración de actividad en la muestra será [AE] = 166 µM/min × 10 ml / 0.4 ml = 4.15 mM/min )
| [sustrato] | ѵ0 | |
|---|---|---|
| (mM) | (µM/min) | |
| sin I | con I | |
| 0.10 | 2.8 | 1.8 |
| 0.15 | 3.6 | 2.4 |
| 0.20 | 4.3 | 2.9 |
| 0.50 | 6.3 | 5.5 |
| 0.75 | 7.4 | 6.5 |
| 1.50 | 9.3 | 8.1 |
En un experimento en el que se midió la velocidad inicial de reacción (usando concentración constante de enzima y concentraciones variables de sustrato), tanto en presencia (220 µM) como en ausencia de un inhibidor, se obtuvieron los resultados que se muestran en la tabla.
a) Con estos datos determina ѵmáx y Km en ausencia de inhibidor.
b) Determina también ѵmáx y Km aparente en presencia del inhibidor.
c) ¿De qué tipo de inhibidor se trata? ¿Qué podemos decir de su mecanismo de interacción con la enzima?
a) ѵmáx = 11.1 µM/min ±0.6; Km = 0.35 mM ±0.05
b) ѵmáx = 11.3 µM/min ±0.6; Km = 0.57 mM ±0.06
c) Como ѵmáx no se modifica y Km aparente aumenta, el inhibidor es competitivo con el sustrato
| [sustrato] | ѵ0 | |
|---|---|---|
| (µM) | (µM/min) | |
| sin I | con I | |
| 3 | 8.4 | 7.4 |
| 5 | 16.5 | 10.7 |
| 10 | 22.5 | 16.0 |
| 30 | 35.2 | 24.0 |
| 90 | 40.5 | 28.8 |
Se estudió la respuesta cinética de una enzima a diferentes concentraciones de sustrato, en presencia y ausencia de un inhibidor I en concentración 2.0 mM. En la tabla se muestran los resultados obtenidos.
a) Con estos datos determina ѵmáx y Km en ausencia de inhibidor.
b) Determina también ѵmáx y Km aparente en presencia del inhibidor.
c) ¿De qué tipo de inhibidor se trata? ¿Qué podemos decir de su mecanismo de interacción con la enzima?
a) ѵmáx = 46 µM/min ±2; Km = 10 mM ±1
b) ѵmáx = 31.8 µM/min ±0.8; Km = 9.7 mM ±0.8
c) Como ѵmáx disminuye y Km apenas varía, el inhibidor es no competitivo, se une a otro sitio de la enzima sn interferir con la unión del sustrato
| [UDP-Glc] | ѵ0 | |
|---|---|---|
| (mM) | (µM UDP/min) | |
| sin ATP | con ATP | |
| 3.0 | 2.0 | 1.8 |
| 6.0 | 4.9 | 3.1 |
| 12.0 | 17.1 | 7.4 |
| 25 | 29.6 | 19.3 |
| 50 | 32.5 | 28.6 |
| 100 | 33.1 | 31.2 |
La enzima glucógeno sintasa cataliza la extensión de moléculas de glucógeno, según la reacción:
UDP-Glc + (Glc)n ![]() UDP + (Glc)n+1
UDP + (Glc)n+1
Se puede seguir el curso de la reacción mediante la medida de UDP liberado. Se preparó una serie de mezclas de reacción (10 ml volumen final) con distintas concentraciones de UDP-Glc, obteniéndose los resultados de velocidad inicial en cada mezcla indicados en la tabla.
El experimento se repitió en presencia de ATP (2.5 mM), con resultados en la misma tabla.
¿Cuál es el efecto del ATP?
sin ATP: ѵmáx = 43 µM/min ±7; Km = 20 mM ±9 pero la curva es más sigmoide que hiperbólica (de ahí, en parte, la elevada imprecisión en los valores)
con ATP: la curva se desplaza hacia la derecha (menor velocidad para una misma concentración de sustrato)
La velocidad máxima es similar, la S50 aumenta, lo que indica reducción de la afinidad aparente. Por tanto, el ATP está ejerciendo una inhibición; dado que ambas curvas son sigmoides, podría tratarse de una enzima alostérica cuyo efector negativo es el ATP.
(Avanzado)
Se quiere medir la actividad de la enzima hexoquinasa, que cataliza la reacción:
| Mg2+ | ||
| glucosa + ATP | glucosa-6P + ADP | |
| hexoquinasa |
El método utilizado mide la formación de glucosa-6P a través de su oxidación instantánea, según la siguiente reacción:
| glucosa-6P + NADP+ | 6P-gluconato + NADPH + H+ | |
| G6P deshidrogenasa |
Como el NADPH muestra absorción de luz a 340nm (ε340 = 6.3 × 106 cm2/mol), se puede seguir el curso de la reacción por espectrofotometría UV.
Se preparó en una cubeta de cuarzo (1 cm de paso óptico) una mezcla de reacción con concentraciones saturantes de todos los sustratos. La reacción se inició añadiendo una muestra problema con hexoquinasa. Se obtuvieron los siguientes datos:
| Tiempo (min) | 0 | 1 | 2 | 3 | 4 | 5 |
| A340 | 0.054 | 0.177 | 0.302 | 0.422 | 0.548 | 0.670 |
a) ¿Cuál fue la velocidad inicial de reacción?
b) Calcula las unidades internacionales (U) de hexoquinasa que hay en 1 ml de mezcla de reacción.
c) ¿Qué ingredientes deben formar la mezcla de reacción?
a) la regresión de los datos da la ecuación A = 0.0541 + 0.1232 t
v = d[P]/dt = dA/dt / (ε × ℓ) = 0.1232 min−1 / ( 6.3×106 cm2/mol × 1 cm ) × 103 cm3/L = 1.96×10−5 M/min = 19.6 µM/min
b) U = µmol/min, por lo que hay 19.6×10−2 U
c) glucosa, ATP, Mg2+, G6P deshidrogenasa, NADP